操作系统的一些算法

操作系统 1 小时 读完 (约 9907 字)

复（yu）习操作系统时做的一些笔记

调度算法

平均等待时间

FCFS（先到先服务）

非抢占的，先请求CPU 的进程先分配到 CPU。FCFS 策略可以用 FIFO 队列来容易地实现。当一个进程进入到就绪队列，其PCB 链接到队列的尾部。当 CPU 空闲时，CPU 分配给位于队列头的进程，接着该运行进程从队列中删除。

SJF（最短作业优先）

优先级调度的一个特例，每个进程与其下一个 CPU 区间段相关联。当 CPU 为空闲

时，它会赋给具有最短 CPU 区间的进程。如果两个进程具有同样长度，那么可以使用 FCFS 调度来处理。

平均等待时间最小（最佳），通过将短进程移到长进程之前，短进程等待时间的减少大于长进程等待时间的增加。

困难：如何知道下一个CPU 区间的长度。

近似：根据上一次实际区间长度和预测长度进行指数平均 $\tau _{n+1} = at_n + (1-a)\tau_n (0 \le a \le 1)$，$a=1$ 时，取决于实际上次实际长度，$a=0$ 时，只与上次预测有关。$a$ 一般为 $1/2$。

抢占 SJF 算法可抢占当前运行的进程，而非抢占 SJF 算法会允许当前运行的进程先完成其 CPU 区间。 抢占 SJF 调度有时称为最短剩余时间优先调度(SRTF，Shortest-Remaining-Time-First scheduling)

优先级调度

每个进程都有一个优先级与其关联，具有最高优先级的进程会分配到 CPU。具有相同优先级的进程按 FCFS 顺序调度。（书上优先级越低，优先程度越高）

当一个进程到达就绪队列时，其优先级与当前运行进程的优先级相比较。如果新到达进程的优先级高于当前运行进程的优先级，那么抢占优先级调度算法会抢占CPU。而非抢占优先级调度算法只是将新进程加到就绪队列的头部。

问题：无穷阻塞(indefinite blocking) 或饥饿 (starvation)。可以运行但缺乏 CPU 的进程可认为是阻塞的，它在等待 CPU 。优先级调度算法会使某个低优先级进程无穷等待 CPU。结果：1. 最终能运行。2. 系统最终崩溃并失去所有未完成的低优先级进程。

解决：老化（aging），逐渐增加在系统中等待很长时间的进程的优先级。

RR（轮转法）

round-robin算法，抢占的，专门为分时系统设计。类似 FCFS，但增加了抢占以切换进程。定义一个较小时间单元，称为时间片（time quan or time slice） 。时间片通常为10~100 ms 。将就绪队列作为循环队列。 CPU 调度程序循环就绪队列，为每个进程分配不超过一个时间片的CPU。

实现：将就绪队列保存为进程的 FIFO 队列。新进程增加到就绪队列的尾部。 CPU 调度程序从就绪队列中选择第一个进程，设置定时器在一个时间片之后中断，再分派该进程。

在极端情况下，如果时间片非常大， 那么 RR 算法与 FCFS 算法一样。如果时间片很小（如 1ms），那么 RR 算法称为处理器共享，（从理论上来说）$n$ 个进程对于用户都有它自己的处理器，速度为真正处理器速度的 $1/n$，实际上因为有上下文切换所以不能太小。

会有上下文切换的额外开销。绝大多数现代操作系统的时间分配为10 ~100ms ，上下文切换的时间一般少于 10μs。 根据经验， 应该有 80% 的 CPU 区间小于时间片。

周转时间也依赖于时间片的大小，通常，如果绝大多数进程能在一个时间片内完成，那么平均周转时间会改善。

多级队列

多级队列调度算法 （multilevel queue scheduling algorithm） 将就绪队列分成多个独立队列。根据进程的属性，如内存大小、进程优先级、进程类型，一个进程被永久地分配到一个队列（优点是低调度开销，缺点是不够灵活）。每个队列有自己的调度算法。

  • 队列之间必须有调度，通常采用固定优先级抢占调度，可能会有饥饿。
  • 队列之间划分时间片。每个队列都有一定的 CPU 时间，这可用于调度队列内的进程 。

多级反馈队列

多级反馈队调度算法 (multilevel feedback queue scheduling algorithm) ，根据不同 CPU 区间的特点以区分进程。如果进程使用过多 CPU 时间，那么它会被转移到更低优先级队列。这种方案将I/O型和交互进程留在更高优先级队列。此外，在较低优先级队列中等待时间过长的进程会被转移到更高优先级队列。这种形式的老化阻止饥饿的发生。

规定优先程度越低则时间片越长（减少CPU型的调度次数）。如果进程因请求I/O，让出了CPU，那么在I/O完成后，进程将进入优先级比I/O请求时离开的队列高(一级)的队列中。

优先程度高的抢占优先程度低的进程。

多级反馈队列调度程序的定义使它成为最通用的 CPU 调度算法。它可被配置以适应特定系统设计。不幸的是，由于需要一些方法来选择参数以定义最佳的调度程序，它也是最复杂的算法。

临界区问题

Peterson算法

由于现代计算机体系架构执行基本机器语言指令，如load， store 的不同方式，在某些机器上不一定能正确运行。需要假设load，store是原子操作。

1
2
3
4
5
6
7
8
9
10
do {
    flag[i] = TRUE;
    turn = j;	/* 最后执行，最后进入 */
    while (flag[j] && turn == j);
    
    // critical section
    
    flag[i] = FALSE;
    // reminder section
} while (TRUE);

turn 表示哪个进程可以进入临界期，flag 表示哪个进程准备进入临界区。

TestAndSet

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
lock = FALSE;
waiting[n] = { FALSE };
do {
    waiting[i] = TRUE;
    key = TRUE;
    while (waiting[i] && key)
        key = TestAndSet(&lock);
    waiting[i] = FALSE;
    
    // critical section
    
    j = (i + 1) % n;
    while ((j != i) && !waiting[j])
        j = (j + 1) % n;
    if (j == i)
        lock = FALSE;
    else
        waiting[j] = FALSE;
    // reminder section
} while (TRUE);

信号量（semaphore）

互斥：

1
2
3
4
5
6
7
8
semaphore mutex = 1;

do {
    wait(mutex);
    // critical section
    signal(mutex);
    // reminder section
} while (TRUE)

同步：

1
semaphore mutex = 1;
1
2
// S1
signal(mutex);
1
2
wait(mutex);
// S2

经典同步问题

有限缓冲问题

empty表示空缓冲项，full表示满缓冲项

1
2
3
// share
semaphore mutex = 1;
int empty = n, full = 0;
1
2
3
4
5
6
7
8
9
10
11
12
13
// producer
do {
    ...
    // produce an item
    ...
    wait(empty);
    wait(mutex);
    ...
    // add item
    ...
    signal(mutex);
    signal(full);
} while (TRUE);
1
2
3
4
5
6
7
8
9
10
// consumer
do {
    wait(full);
    wait(mutex);
    ...
    // remove an item
    ...
    signal(mutex);
    signal(empty);
} while (TRUE);

读者-写者问题

读者优先：

1
2
3
// share
semaphore mutex = 1, wrt = 1;
int readcount = 0;
1
2
3
4
5
6
7
8
// writer
do {
    wait(wrt);
    ...
    // writing
    ...
    signal(wrt);
} while (TRUE);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// reader
do {
    wait(mutex);
    ++readcount;
    if (readcount == 1)
        wait(wrt);
    signal(mutex);
    ...
    // reading
    ...
    wait(mutex);
    --readcount;
    if (readcount == 0)
        signal(wrt);
    signal(mutex);
} while (TRUE);

写者优先：

1
2
3
// share
int readcount = 0, writecount = 0;
semaphore rmutex = 1, wmutex = 1, readTry = 1, resource = 1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// writer
do {
    wait(wmutex);
    ++writecount;
    if (writecount == 1)
        wait(readTry);
    signal(wmutex);
    
    wait(resource);
    // writing
    signal(resource);
    
    wait(wmutex);
    --writecount;
    if (writecount == 0)
        signal(readTry);
    signal(wmutex);
} while (TRUE);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
do {
    wait(readTry);
    wait(rmutex);
    ++readcount;
    if (readcount == 1)
        wait(resource);
    signal(rmutex);
    signal(readTry);
    
    // reading
    
    wait(rmutex);
    --readcount;
    if (readcount == 0)
        signal(resource);
    signal(rmutex);
} while (TRUE);

平等：

1
2
3
// share
int readcount = 0;
semaphore resource = 1, readCountAccess = 1, serviceQueue = 1;
1
2
3
4
5
6
7
8
// writer
do {
    wait(serviceQueue);
    wait(resource);
    signal(serviceQueue);
    // writing
    signal(resource);
} while (TRUE);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// reader
do {
    wait(serviceQueue);
    wait(readCountAccess);
    if (readcount == 0)
        wait(resource);
    ++readcount;
    signal(serviceQueue);
    signal(readCountAccess);
    // reading
    wait(readCountAccess);
    --readCount;
    if (readCount == 0)
        signal(resource);
    signal(readcountAccess);
} while (TRUE);

哲学家就餐问题

无法解决饿死问题。

方案1：先拿编号小的筷子

1
2
3
4
5
6
7
8
9
10
do {
    int m = min(i, (i + 1) % 5);
    int n = max(i, (i + 1) % 5);
    wait(chopstick[m]);
    wait(chopstick[n]);
    // eat
    signal(chopstick[i]);
    signal(chopstick[(i + 1) % 5]);
    // think
} while (TRUE)

方案2：最多只允许4个哲学家同时坐在桌子上。

方案3：只有当两根筷子都空闲时才允许拿起。

理发师问题

1
2
3
// share
semaphore barberReady = 0, accessWRSeats = 1, custReady = 0;
int WRSeets = N;
1
2
3
4
5
6
7
8
9
// barber
do {
    wait(custReady);
    wait(accessWRSeets);
    ++WRSeets;
    signal(barberReady);
    signal(accessWRSeets);
    // cut hair
} while (TRUE);
1
2
3
4
5
6
7
8
9
10
11
12
// customer
wait(accessWRSeets);
if (WRSeets > 0) {
    --WRSeets;
    signal(custReady);
    signal(accessWRSeets);
    wait(barberReady);
    // have hair cut
} else {
    signal(accessWRSeets);
    // leave
}

死锁

资源分配图

每种资源都只有单个实例时，有环是充分必要条件；多个实例时，有环是必要条件。

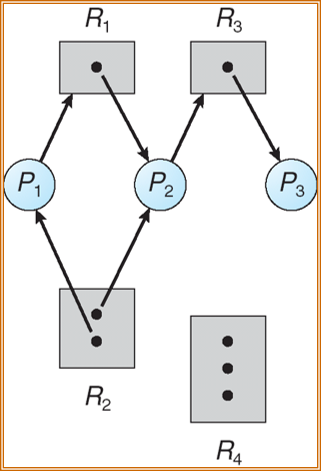
资源分配图算法

适用于每种资源只有单个实例

资源分配图：在资源分配图中加入需求边，以虚线表示。系统必须事先说明所要求的资源，即当进程 $P_i$ 开始执行时，所有需求边必须先处于资源分配图。可放宽这个条件，以允许只有在进程 $P_i$ 的所有相关的边都为需求边时才将需求边 $P_i \to R_j$ 增加到图中。

内容：假设进程 $P_i$ 申请资源 $R_j$。只有在将申请边 $P_i$ 变成分配边 $P_i$ 而不会导致资源分配图形成环时，才允许申请。 代价为$O(n^2)$。

银行家算法

  • Available：长度为 $m$ 的向量，表示每种资源的现有实例的数量。如果 $Available[j]=k$ ，那么资源$R_j$现有 $k$ 个实例。
  • Max：$n \times m$ 矩阵，定义每个进程的最大需求。如果 $Max[i][j]=k$，那么进程 $P_i$最多可以申请 $k$ 个资源类型 $R_j$ 的实例。
  • Allocation：$n \times m$ 矩阵，定义每个进程现在所分配的各种资源类型的实例数量。如果 $Allocation[i][j]=k$，那么进程 $P_i$ 现在已分配了 $k$ 个资源类型 $R_j$ 的实例。
  • Need：$n \times m$ 矩阵，表示每个进程还需要的剩余的资源。如果 $Need[i][j] = k$，那么进程 $P_i$ 还可能申请 $k$ 个资源类型 $R_j$ 的实例。注意，$Need[i][j] = Max[i][j] - Allocation[i][j]$。

$Allocation_i$ 表示分配给 $P_i$ 的资源；$Need_i$ 表示进程为完成其任务可能需要申请的额外资源。

向量 $X \le Y$ 当且仅当 $X[i] \le Y[i]$。

安全性算法

确定系统是否处于安全状态。

  1. 设 $Work$ 和 $Finish$ 分别为长度为 $m$ 和 $n$ 的向量。按如下方式进行初始化，$Work=Available$ 且 $\text{for}\ i=0,1,\ldots ,n-1,Finish[i]=false$。

  2. 查找这样的 $i$ 满足使其满足

    1. $Finish[i]=false$
    2. $Need_i \le Work$

    如果没有这样的 $i$ 存在，那么就转到第4步。

  3. $Work = Work + Allocation_i$，$Finish[i]=true$，返回到第2步

  4. 如果对所有 $i$，$Finish[i]=true$，那么系统处于安全状态。

代价：$O(m \times n^2)$

资源请求算法

判断是否可安全允许请求。

设 $Request_i$ 为进程 $P_i$ 的请求向量。如果 $Request_i[j] == k$，那么进程 $P_i$ 需要资源类型 $R_j$ 的实例数量为 $k$。当进程 $P_i$ 作出资源请求时，采取如下动作。

  1. 如果 $Request_i \le Need_i$，那么转到第2步，否则产生出错条件，因为进程 $P_i$ 已超过了其最大请求。

  2. 如果 $Request_i \le Available$，那么转到第3步，否则，$P_i$ 必须等待，因为没有可用资源。

  3. 假定系统可以分配给进程 $P_i$ 所请求的资源，并按如下方式修改状态：

    $ Available=Available-Request_i$

    $Allocation_i=Allocation_i+Request_i$

    $Need_i=Need_i-Request_i$

如果所产生的资源分配状态是安全的，那么交易完成且进程 $P_i$ 可分配到其所需要资源。然而，如果新状态不安全，那么进程 $P_i$ 必须等待 $Request_i$ 并恢复到原来资源分配状态。

死锁检测

单实例

等待（wait-for）图：等待图有一条 $P_i \to P_j$的边，当且仅当相应的资源分配图中包含两条边 $P_i \to R_q$ 和 $R_q \to P_j$，其中 $R_q$ 为资源。

当且仅当有环时死锁，$O(n^2)$

多实例

  • Available：长度为 $m$ 的向量，表示每种资源的现有实例的数量。如果 $Available[j]=k$ ，那么资源$R_j$现有 $k$ 个实例。
  • Allocation：$n \times m$ 矩阵，定义每个进程现在所分配的各种资源类型的实例数量。如果 $Allocation[i][j]=k$，那么进程 $P_i$ 现在已分配了 $k$ 个资源类型 $R_j$ 的实例。
  • Request：$n \times m$ 矩阵，表示当前每个进程的资源请求情况。如果 $Request[i][j] = k$，那么进程 $P_i$ 现在正在请求 $k$ 个资源类型 $R_j$ 的实例。

  1. 设 $Work$ 和 $Finish$ 分别为长度为 $m$ 和 $n$ 的向量。初始化 $Work=Available$。对 $i = 0,1,\ldots,n-1$，如果 $Allocation_i$不为0，则$Finish[i]=false$，否则为 $true$

  2. 找到满足下面条件的 $i$：

    1. $Finish[i]=false$
    2. $Request_i\le Work$

    如果没有这样的 $i$，则转到第4步。

  3. $Work=Work+Allocation_i$，$Finish[i]=true$，转到第2步

  4. 如果对某个 $i(0 \le i \lt n)$，$Finish[i]=false$，则系统处于死锁状态，而且，如果$Finish[i]=false$，则进程 $P_i$ 死锁。

代价：$O(m \times n^2)$

内存

动态存储分配问题

  • 首次适应：分配第一小足够大的孔。查找可以从头开始，也可以从上次首次适应结束时开始。一旦找到足够大的空闲孔，就可以停止。
  • 最佳适应：分配最小的足够大的孔。必须查找整个列表，除非列表按大小排序。这种方法可以产生最小剩余孔。
  • 最差适应：分配最大的孔。同样，必须查找整个列表，除非列表按大小排序。这种方法可以产生最大剩余孔，该孔可能比最佳适应方法产生的较小剩余孔更为有用。

比较：首次适应和最佳适应在执行时间和利用空间方面都好于最差适应；首次适应和最佳适应在利用空间方面难分伯仲，但是首次适应方法更快些。

最佳适应和首次适应都存在外碎片问题。

50%规则：对采用首次适应方法的统计说明，不管使用什么优化，假定有 $N$ 个可分配块，那么可能有 $0.5N$ 个块为外部碎片。即 $1/3$ 的内存可能不能使用。

分页

页号 $\to$ 页表 $\to$ 帧号

存在内碎片但不存在外碎片。

TLB：$EAT=\alpha(m+n)+(1-\alpha)(2m+n)$，其中 $\alpha$ 为命中率，$n$ 为快表访问时间，$m$为内存访问单位时间。

页表结构

  1. 层次页表（两（三…）级分页算法）：将页表再分页。向前映射页表（forward-mapped page table）

    变种：VAX结构（分区）

  2. 哈希页表：每个元素有3个域：虚拟页码，所映射的帧号，指向链表下一个元素的指针。

    算法：虚拟（逻辑）地址中的虚拟页号转换到哈希表中，用虚拟页号与链表中的每个元素的第一个域相比较。如果匹配，那么相应的帧号(第二个域)就用来形成物理地址；如果不匹配，那么就对链表中的下一个节点进行比较，以寻找一个匹配的页号。

    变种：群集页表（clustered page table）每一条目不只包括一页信息，而是包括多页。

  3. 反向页表：对于每个真正的内存页或帧才有一个条目。整个系统只有一个页表，对每个物理内存的页只有一条相应的条目。

    简化的反向页表实现：系统的每个虚拟地址有一个三元组 <pid, page-number, offset>

分段

虚拟地址：<segment-number, offset>

段表：<base, limit>，STBR，STLR

  1. 重定位：动态重定位。
  2. 分享：分享段号。
  3. 申请空间：首次适应/最佳适应，会有外碎片。

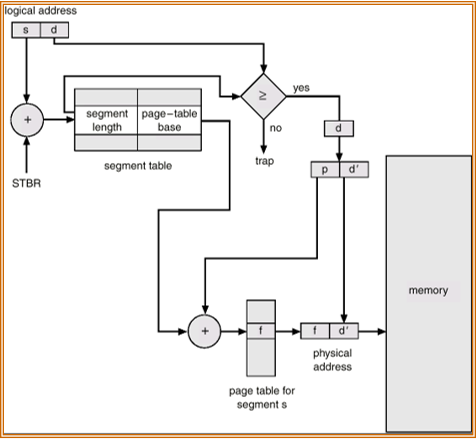
段页式（Segmentation with Paging）

MULTICS：段表保存页表基址（而不是段基址）。

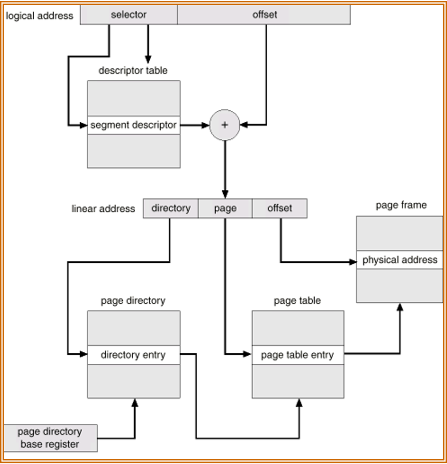
Intel 386：分段 + 两级分页。

虚拟内存

处理页错误陷阱：

  1. 检查进程的内部页表（通常与PCB 一起保存），以确定该引用是合法还是非法的地址访问。
  2. 如果引用非法，那么终止进程。如果引用有效但是尚未调入页面，那么现在应调入。
  3. 找到一个空闲帧（例如，从空闲帧链表中选取二个）。
  4. 调度一个磁盘操作，以便将所需要的页调入刚分配的帧。
  5. 当磁盘读操作完成后，修改进程的内部表和页表，以表示该页己在内存中。
  6. 重新开始因陷阱而中断的指令。进程现在能访问所需的页，就好像它似乎总在内存中。

按需调页

$$
EAT = (1 - p) \times ma + p \times (\text{page fault overhead} + [\text{ swap page out }] + \text{swap page in} + \text{restart overhead})
$$

$p$ 为页错误概率，$ma$ 为内存访问时间（10 ~ 200ns）。换出不一定需要。

页置换算法

FIFO

FIFO 页置换算法为每个页记录着该页调入内存的时间。当必须置换一页时，将选择最旧的页。

Belady异常：页错误率可能会随着所分配的帧数的增加而增加。

最优置换

最优页置换算法是所有算法中产生页错误率最低的，且绝没有 Belady异常 的问题。被称为 OPT 或 MIN。

它会置换最长时间不会使用的页（未来一段时间）。

难以实现，用于比较研究。

LRU

最近最少使用算法。置换最长时间没有使用的页（过去一段时间）。

实现：

  • 计数器：对每次内存引用，计数器都会增加。每次内存引用时，时钟寄存器的内容会被复制到相应页所对应页表工页的使用时间域内。置换时需要搜索。
  • 栈：每当引用一个页，该页就从栈中删除并放在顶部。所以该栈可实现为具有头指针和尾指针的双向链表。这样，删除一页并放在栈顶部在最坏情况下需要改变6个指针。更新费时，但是置换时不需要搜索。

栈算法

最优置换和 LRU置换 都没有 Be1ady异常。这两个都属于同一类算法，称为栈算法(stack algorithm) 。对于帧数为 $n$ 的内存页集合永远是对于帧数为 $n+1$ 的内存页集合的子集。对于LRU 算法，如果内存页的集合为最近引用的页，那么对于帧的增加，这 $n$ 页仍然为最近引用的页，所以也仍然在内存中。

需要有硬件的支持，否则时间开销会很大。

近似LRU页置换

页表内的每项都关联着一个引用位（reference bit）。每当引用一个页时（无论是对页的字节进行读或写），相应页表的引用位就被硬件置位。

附加引用位算法

在规定时间间隔里记录引用位。例如，如果移位寄存器含有00000000，那么该页在8个时间周期内没有使用；如果移位寄存器的值为11111111，那么该页在过去每个周期内都至少使用过一次。具有值为11000100的移位寄存器的页要比值为01110111的页更为最近使用。如果将这8位作为无符号整数，那么具有最小值的页为 LRU 页，且可以被置换。注意这些数字并不唯一，可以置换所有具有最小值的页，或在这些页之间采用 FIFO 来选择置换。

二次机会算法

二次机会置换的基本算法是 FIFO 置换算法。当要选择一个页时，检查其引用位。如果其值为0，那么就直接置换该页。如果引用位为1，那么就给该页第二次机会，并选择下一个 FIFO 页。当一个页获得第二次机会时，其引用位清零，且其到达时间设为当前时间。

可以采用循环队列（也称时钟算法）。最坏时所有位均已置位，此时算法退化为 FIFO。

增强型二次机会算法

对引用位和脏位同时考虑：

  • $(0,0)$，最近没有使用也没有修改——用于置换的最佳页
  • $(0,1)$，最近没有使用但修改过——不是很好，因为在置换之前需要将页写出到磁盘。
  • $(1,0)$，最近使用过但没有修改一一它有可能很快又要被使用。
  • $(1,1)$，最近近使用过且修改过一一它有可能很快又要被使用，且置换之前需要将页写出到磁盘。

使用时钟算法时判断类型，替换第一个符合的（由上往下优先级越低）。

基于计数的页置换

为每个页保留一个用于记录其引用次数的计数器。实现费时，且不能很好的近似OPT。

LFU

最不经常使用页置换算法：置换计数最小的页。

问题：一个页在进程开始时使用很多，但以后就不再使用。由于其使用过很多，所以它有较大次数，所以即使不再使用仍然会在内存中。

解决：定期地将次数寄存器右移一位，以形成指数衰减的平均使用次数。

MFU

最常使用页置换算法，基于如下理论：具有最小次数的页可能刚刚调进来，且还没有使用。

页缓冲算法

系统通常保留一个空闲帧缓冲池。当出现页错误时，会像以前一样选择一个牺牲帧。然而，在牺牲帧写出之前，所需要的页就从缓冲地中读到空闲内存。这种方法允许进程尽可能快地重启，而无须等待牺牲帧页的写出。当在牺牲帧以后写出时，它再加入到空闲帧池。

扩展：

  • 维护一个己修改页的列表。每当调页设备空闲时，就选择一个修改页井写到磁盘上，接着重新设置其修改位。这种方案增加了当需要选择置换时干净页的概率而不必写出。
  • 保留一个空闲帧池，但要记住哪些页在哪些帧中。由于当帧写到磁盘上时其内容并没有修改，所以在该帧被重用之前如果需要使用原来页，那么原来页可直接从空闲帧池中取出来使用。这时并不需要 I/O 。当一个页错误发生时，先检查所需要页是否在空闲帧池中。如果不在，那么才必须选择一个空闲帧来读入所需页。

帧分配

  • 平均分配
  • 按比例分配

分配随着多道程序程度变化。如果考虑优先级，则按比例可以根据优先级大小分配，或进程大小和优先级的组合（此时称优先级分配，不考虑则称固定分配）。

  • 全局置换，一个进程可以从另一个进程中拿到帧。

    缺点：不能控制页错误率。

    优点：更好的系统吞吐量。

  • 局部置换，要求每个进程仅从其自己的分配帧中进行选择。

    缺点：不能用其他进程的不常用的内存。

  • 局部模型，如果分配的帧数少于现有局部的大小，那么进程会颠簸。
  • 工作集合模型，防止了颠簸，并尽可能地提高了多道程序的程度。因此，它优化了 CPU 使用率。困难是难以追踪工作集合，可以通过固定定时中断和引用位近似模拟。
  • 页错误频率（PPF），设置上限和下限。太高时分配帧；太低时移走帧。

文件系统

目录结构

  • 单层结构目录，命名困难，不能分组。
  • 双层结构目录，允许不同目录有相同名字的文件，搜索更有效率，共享困难。
  • 树状结构目录，允许分组，搜索更有效率。
  • 无环图结构目录，允许分享。更灵活，但是删除需要谨慎处理。
  • 通用图结构目录，同样有删除的问题。

分层文件系统

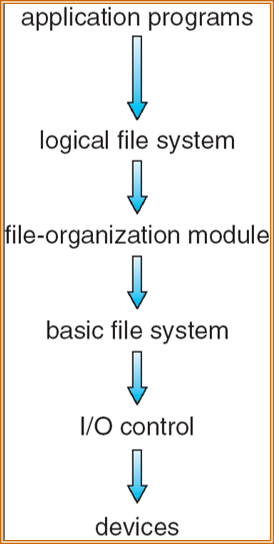
逻辑文件系统和文件组织模块为文件系统单独拥有，基本文件系统和 I/O 控制可以共用

VFS

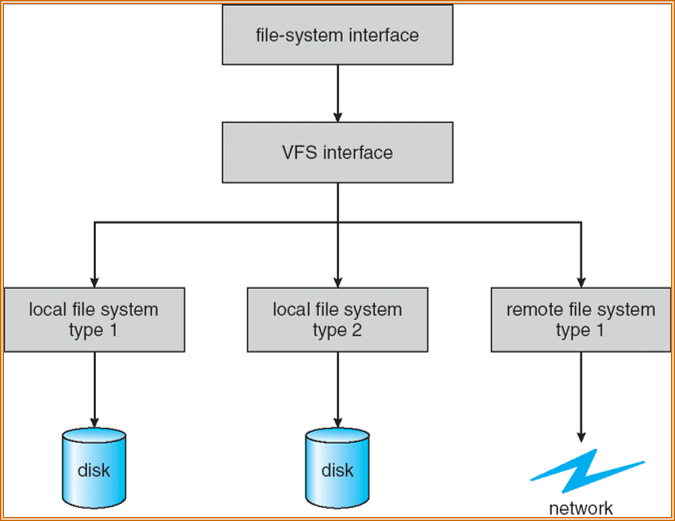
对不同的文件类型分配一系列操作，调用相应的函数指针（指向函数表），从而不关心文件类型

  • 索引节点对象（inode object）表示一个单独的文件对象。
  • 文件对象（file object）表示一个打开的文件。
  • 超级块对象（superlock object）表示整个文件系统。
  • 目录条目对象（dentry object）表示一个单独的目录条目。

目录实现

  • 线性表，简单但是费时。
  • 哈希表，加快了搜索时间，简化了插入删除，但要解决冲突问题和固定大小问题。

分配方法

连续分配

要求每个文件在磁盘上占有一组连续的块。

用于访问连续分配文件所需要的寻道数最小，在确实需要寻道时所需要的寻道时间也最小。

问题：为新文件找到空间。

可以使用动态存储分配，首次适合和最优适合都要比最坏适合更为高效。首次适合和最优适合在空间使用方面不相上下，但是首次适合运行速度更快。但存在外碎片。可以试用合并，但是用时很长，在线合并会使性能明显下降。

问题：确定文件需要的空间大小。

  • 可以终止用户程序，并加上合适的错误消息。用户必须分配更多空间并再次运行程序。这些重复运行可能代价很高。为了防止这些问题，用户通常会过多地估计所需的磁盘空间，从而导致了空间浪费。
  • 找一个更大的孔，复制文件内容到新空间，释放以前的空间。只要空间存在这些动作就可以重复，不过这比较耗费时间。

会存在内碎片。

可以使用扩展，该方案开始分配一块连续空间，当空间不够时，另一块被称为扩展(extent)的连续空间会添加到原来的分配中。文件块的位置就成为开始地址、块数、加上一个指向下一扩展的指针。如果扩展太大，内部碎片可能仍然是个问题；随着不同大小的扩展的分配和删除，外部碎片可能也是个问题。

链接分配

链接分配 （linked allocation） 解决了连续分配的所有问题。采用链接分配，每个文件是磁盘块的链表；磁盘块分布在磁盘的任何地方。目录包含文件第一块的指针和最后一块的指针。

没有外碎片。

缺点：

  • 只能顺序访问。

  • 指针需要空间。

    解决方法：多个块组成簇，并按簇而不是按块来分配。减少指针个数。

  • 可靠性，由于文件时通过指针链接的，而指针分布在整个磁盘上，如果指针丢失或损坏会导致链接空闲空间列表或另一个文件，一个不彻底的解决方案是使用双向链表或在每个块中存上文件名和相对块数。

变种

使用文件分配表（FAT），每个卷的开始部分用于存储该 FAT 。每块都在该表中有一项，该表可以通过块号码来索引。 目录条目包含有文件首块的块号码。根据块号码索引的 FAT 条目包含文件下一块的块号码。这条链会一直继续到最后一块，该块对应 FAT 条目的值为文件结束值。

如果不对 FAT 采用缓存，FAT 分配方案可能导致大量的磁头寻道时间。磁头必须移到卷的开头以便读入 FAT，寻找所需要块的位置，接着移到块本身的位置。在最坏的情况下，每块都需要移动两次。其优点是改善了随机访问时间，因为通过读入 FAT 信息，磁头能找到任何块的位置。

索引分配

索引分配 （indexed allocation） 通过把所有指针放在一起，即通过索引块解决了链接分配不能有效支持直接访问（没有FAT时）的问题。

优点：索引分配支持直接访问，且没有外部碎片问题，这是因为磁盘上的任一块都可满足更多空间的要求。

缺点：索引分配会浪费空间。索引块指针的开销通常要比链接分配指针的开销大。

索引的大小：

  • 链接方案：二个索引块通常为一个磁盘块。因此，它本身能直接读写。为了处理大文件，可以将多个索引块链接起来。

  • 多层索引：链接表示的一种变种是用第一层索引块指向一组第二层的索引块，第二层索引块再指向文件块。

  • 组合方案：参考 UFS 的 inode

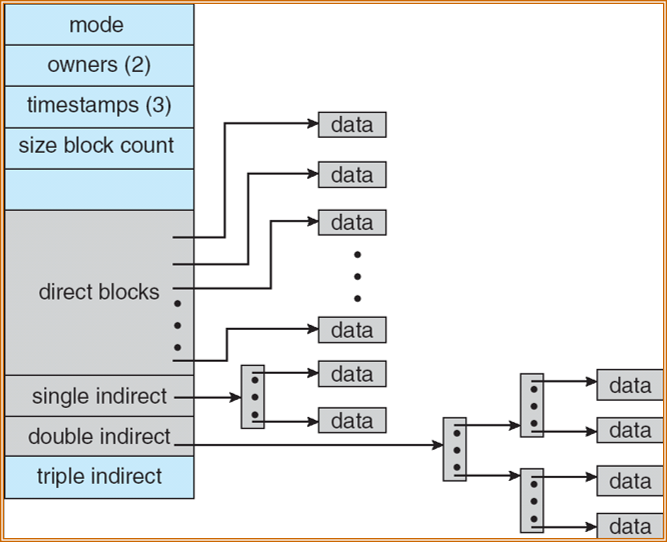
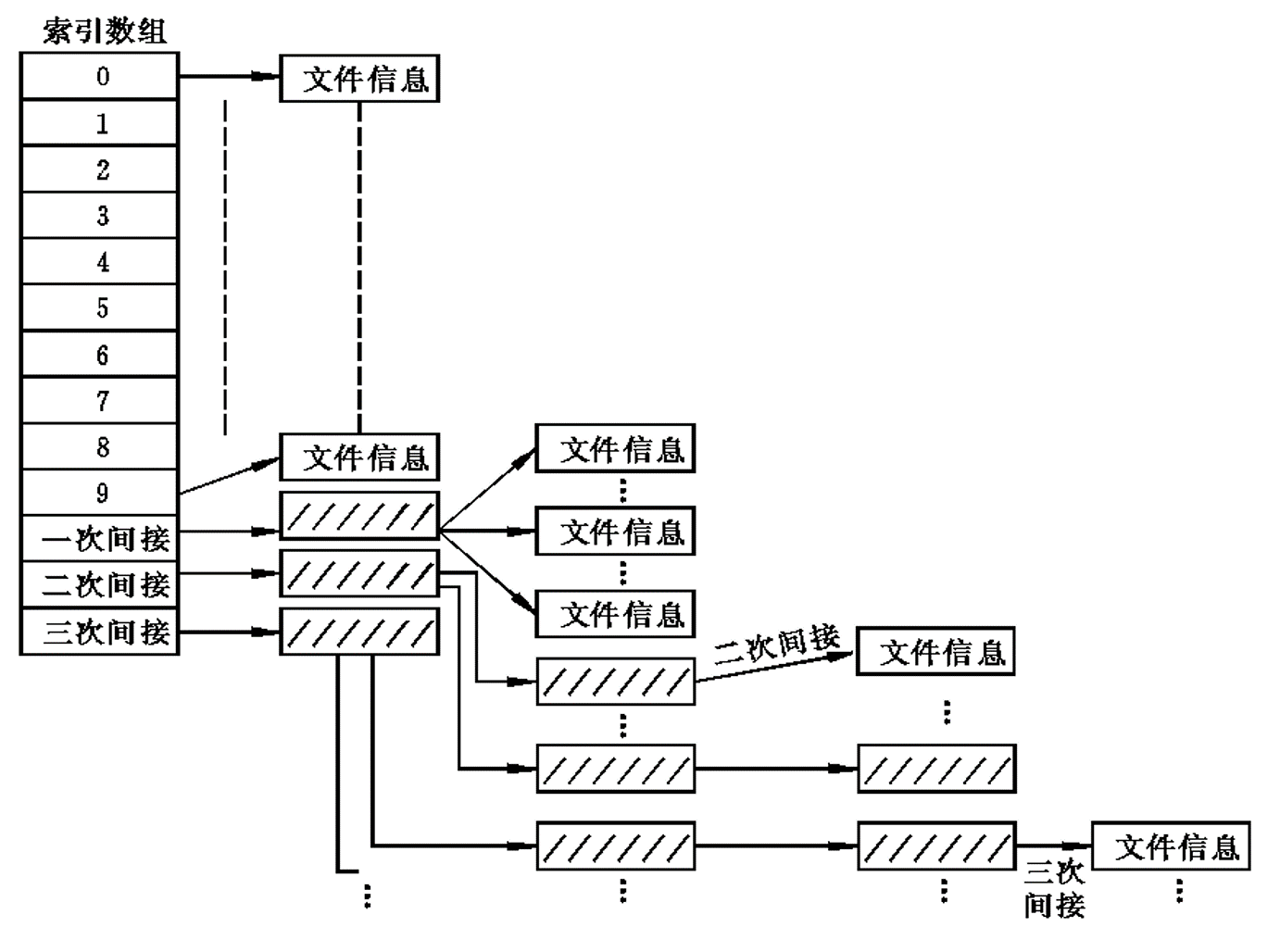
索引分配方案与链接分配一样在性能方面有所欠缺。特别是，虽然索引块可以缓存在内存中，但是数据块可能分布在整个分区上。

空闲空间管理

位图/位向量

通常，空闲空间表实现为位图 （bit map）或位向量（bit vector）。每块用一位表示。如果一块为空闲，那么其位为 1；如果一块已分配，那么其位为 0。

计算：$(\text{number of bits per word}) \times (\text{number of 0-value words})+\text{offset of first 1 bit}$

优点：查找磁盘上第一个空闲块和 $n$ 个连续空闲块时相对简单和高效。

缺点：除非整个位向量都能保存在内存中（井时而写入到磁盘用于恢复的需要），否则位向量的效率就不高（大磁盘不适宜）

链表

将所有空闲磁盘块用链表连接起来，并将指向第一空闲块的指针保存在磁盘的特殊位置，同时也缓存在内存中。

遍历时效率不高，需要大量的 I/O。

FAT 方法将空闲块的计算结合到分配数据结构中，不再需要另外的方法。

组

对空闲链表的一个改进是将 $n$ 个空闲块的地址存在第一个空闲块中。这些块中的前 $n-1$ 个确实为空，而最后一块包含另外 $n$ 个空闲块的地址，如此继续。

计数

通常，有多个连续块需要同时分配或释放，尤其是在使用连续分配和采用簇时更是如此。因此，不是记录 $n$ 个空闲块的地址，而是可以记录第一块的地址和紧跟第一块的连续的空闲块的数量 $n$。这样，空闲空间表的每个条目包括磁盘地址和数量。虽然每个条目会比原来需要更多空间，但是表的总长度会更短，这是 因为连续块的数量常常大于 l 。

磁盘调度

FCFS

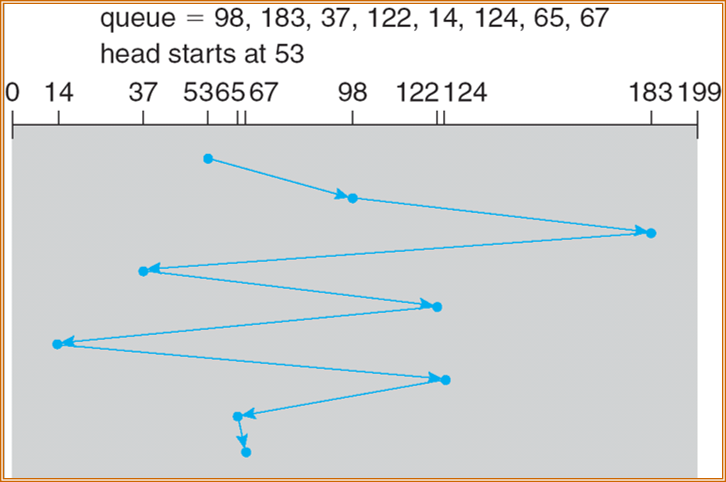
SSTF

最短寻道时间优先算法（shortest-seek-time-first, SSTF），选择距当前磁头位置由最短寻道时间的请求来处理。类似于最短作业优先（SJF），可能导致“饥饿”。

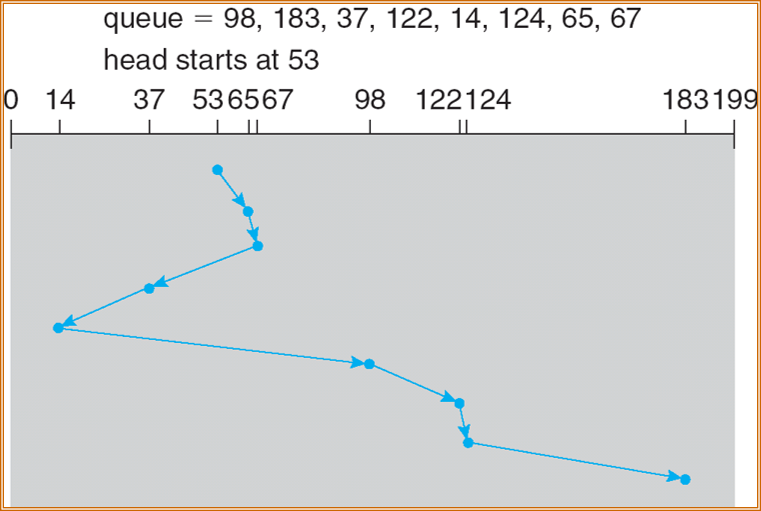
SCAN

也被称为电梯算法（elevator algorithm），磁臂从磁盘的一端向另一端移动，同时当磁头移过每个柱面时，处 理位于该柱面上的服务请求。当到达另一端时，磁头改变移动方向，处理继续。

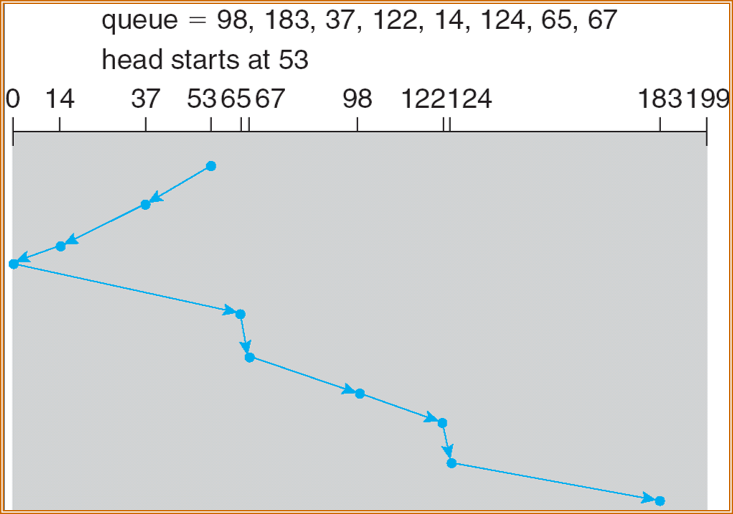
C-SCAN

Circular SCAN，提供一个更为均匀的等待时间。与 SCAN 一样，C-SCAN 将磁头从磁盘一端移到磁盘的另一端，随着移动不断地处理请求。不过，当磁头移到另一端时，它会马上返回到磁盘开始，返回时并不处理请求。

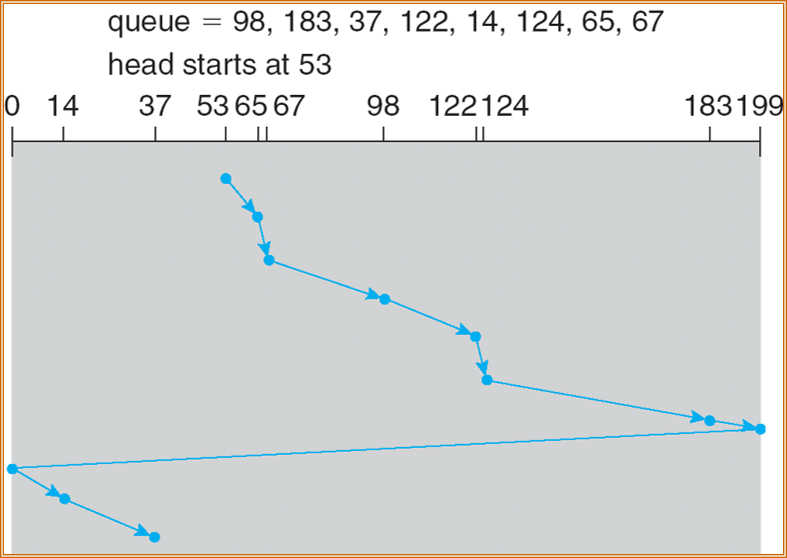
LOOK/C-LOOK

类似 SCAN/C-SCAN，但是磁头只移动到一个方向上最远的请求为止。它们在朝一个方向移动会看 （look） 是否有请求。

C-LOOK：

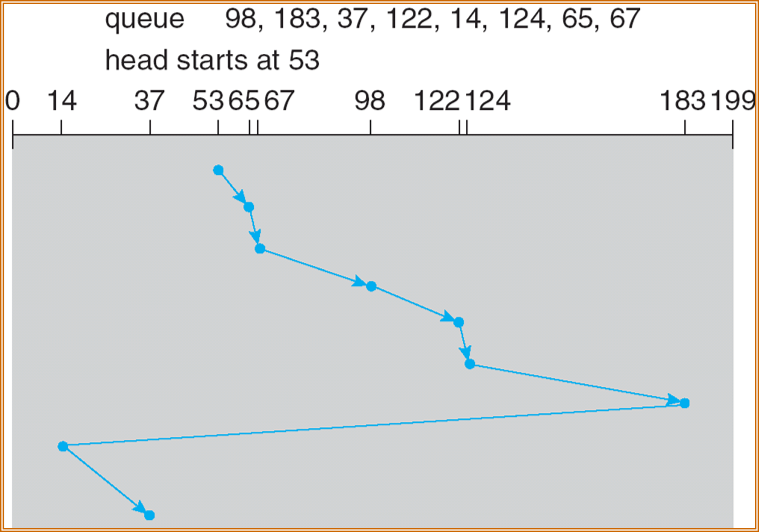
RAID

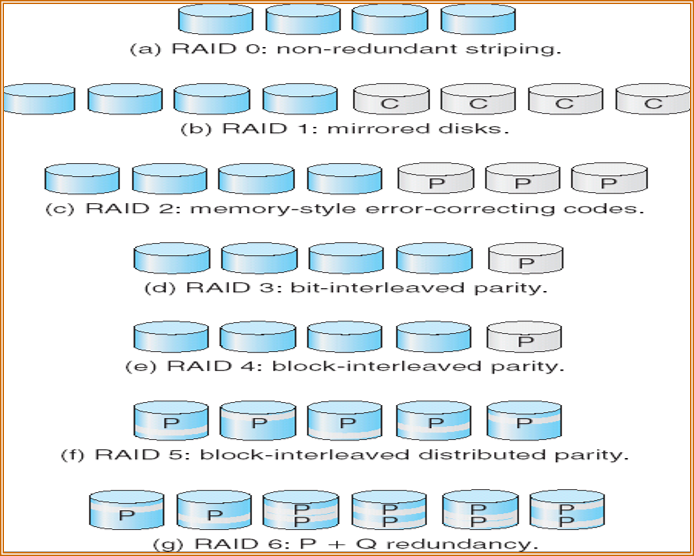
C：数据的第二副本，P：纠错位

  • RAID 0：按块级分散的磁盘阵列，没有冗余。
  • RAID 1：磁盘镜像。
  • RAID 2：也称内存方式的差错纠正代码结构，如果一个磁盘出错，那么可从其他磁盘中读取字节的其他位和相关差错纠正位，以重新构造被损坏的数据。注意，对于 4 个磁盘的数据， RAID 4级别只用了 3 个额外磁盘，而 RAID 1 级别则需要用 4 个额外磁盘。在实际中不使用
  • RAID 3：又称位交织奇偶结构，如果一个扇区损坏，那么知道是哪个扇区，通过计算其他磁盘 扇区相应位的奇偶值可得出所损坏位是 1 还是 0。
  • RAID 4：又称块交织奇偶结构，采用块级分散，另外在一独立磁盘上保存其他 $N$ 个磁盘相应块的奇偶块。
  • RAID 5：又称块交织分布奇偶结构，将数据和奇偶分布在所有 $N+l$ 块磁盘上。例如，对于 $5$ 个磁盘的阵列，第 $n$ 块的奇偶保存在磁盘 $(n\ \text{mod}\ 5)+1$ 上。
  • RAID 6：也称为P+Q冗余方案，与 RAID 5相似，但是使用差错纠正码和Read-Solomon码。图中的方案为每 4 个位的数据使用了 2 个位的冗余数据，而不是像级别 5 那样的一个奇偶位，这样系统可以容忍两个磁盘出错。
  • RAID 0+1：RAID 0 提供了性能，而 RAID 1 提供了可靠性。一组磁盘被分散成条，每一条再镜像到另一条。
  • RAID 1+0：先镜像，再分条。

I/O 子系统

I/O操作调度：设备状态表配备等待队列。

缓冲

缓冲区是用来保存两个设备之间或在设备和应用程序之间所传输数据的内存区域。采用缓冲的三种理由：

  • 处理数据流的生产者与消费者之间的速度差异。双缓冲将生产者与消费者进 行分离解楠，因而缓和两者之间的时序要求。
  • 协调传输数据大小不一致的设备。缓冲常常用来处理消息的分段和重组。
  • 支持应用程序 I/O 的复制语义。根据“复制语义”，操作系统保证要写入磁盘的数据就是 write()系统调用发生时的版本，而无须顾虑应用程序缓冲区随后发生的变化。一个简单方法就是操作系统在 write() 系统调用返回到应用程序之前将应用程序缓冲区复制到内核缓冲区中。

高速缓存

高速缓存（cache） 是可以保留数据副本的高速存储器。高速缓冲区副本的访问要比原始数据访问要更为高效。

缓冲与高速缓存的差别是缓冲可能是数据项的唯一的副本，而根据定义高速缓存只是提供了一个驻留在其他地方的数据在高速存储 上的一个副本。

假脱机

假脱机（Spooling）是用来保存设备输出的缓冲区，这些设备（如打印机）不能接收交叉的数据流。

用程序的输出先是假脱机到一个独立的磁盘文件上。当应用程序完成打印时，假脱机系统将对相应 的待送打印机的假脱机文件进行排队。假脱机系统一次复制一个己排队的假胁机文件到打印机上。

#note #algorithm #OS
【week1】55. Jump Game 解题报告 Vi, java, Ant, Junit自学报告

评论

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×