前言
emmm,也没什么说的,归并排序和快速排序都是一种“分而治之”的思想实现,所以就一起说了,至于堆排序就不说了,毕竟我还要写二项队列。。
归并排序
归并排序的核心思想很简单:把数组对半拆分->分别排序->有序合并。明白了这个就可以采用递归来实现,基准条件就是数组为空时。(虽然这么说但第一次写完全不会。
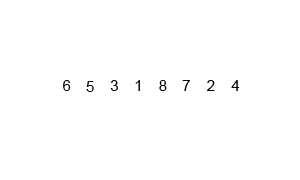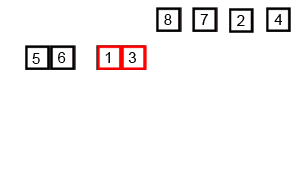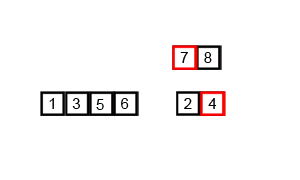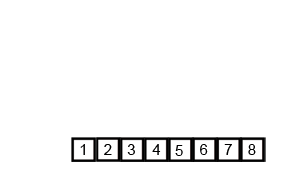
gif By Swfung8
实现
对半拆分是递归实现。有序合并可以使用两个index分别指向要合并的数组,然后根据大小将元素放进temp中(temp为中转数组,整个排序只需要一个)
src
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class MergeSort {
private:
void msort(vector<int> &arr, int temp[], int start, int end) {
if (start < end) {
int center = (start + end) / 2;
msort(arr, temp, start, center);
msort(arr, temp, center + 1, end);
merge(arr, temp, start, center + 1, end);
}
}
void merge(vector<int> &arr, int temp[], int start, int middle, int end) {
int i = start, j = middle, begin = start;
while (i < middle && j <= end)
if (arr[i] > arr[j])
temp[start++] = arr[j++];
else
temp[start++] = arr[i++];
while (i < middle)
temp[start++] = arr[i++];
while (j <= end)
temp[start++] = arr[j++];
for (int k = begin; k <= end; ++k)
arr[k] = temp[k];
}
public:
vector<int>& sort(vector<int> &arr) {
if (!arr.size())
return arr;
int *temp = new int[arr.size() * sizeof(int)];
msort(arr, temp, 0, arr.size() - 1);
return arr;
}
};
|
时间复杂度
假设数组的大小为$N=2^k$,则时间的递推公式为
$$T(1)=1$$
$$T(N)=2T(N/2)+N$$
上式中$T(1)$消耗常数时间,而$T(N)$则消耗将其子数组排序的时间和自身合并的时间。经过计算可得
$$T(N)=NT(1)+N\log N=N\log N+N$$
所以时间复杂度为$O(N\log N)$
快速排序
顾名思义,这个排序很快,是平均情形下最快的已知算法。
快排的核心算法也很简单,假设有一个数组$S$:
- 如果$S$中元素个数为0或1,则返回
- 取$S$任一元素$v$为枢纽元(pivot)
- 将$S-\lbrace v \rbrace$分成两个不相交的集合:$S_1=\lbrace x\in S-\lbrace v\rbrace \mid x\le v\rbrace $和$S_2=\lbrace x\in S-\lbrace v\rbrace\mid x\ge v\rbrace$
- 返回$quicksort(S_1)$后,继随$v$,继而$quicksort(S_2)$,即三者按该顺序存放在$S$中。
换个角度看这个排序,即每次选出一个枢纽元,并将其放在它应该在的地方(排序后的位置)
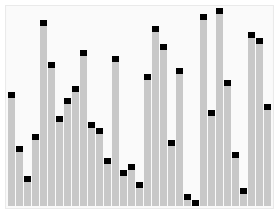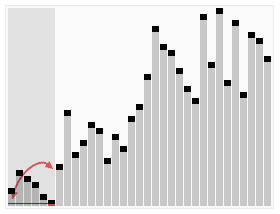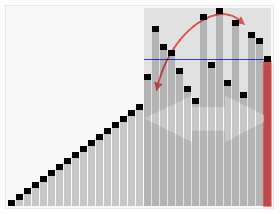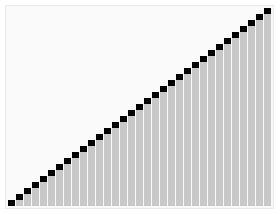
gif By en:User:RolandH
选取枢纽元
最简单的方法或许是直接选取第一个或最后一个元素作为枢纽元,但这样是很糟糕的选法,如果输入为有序数组,则排序将产生一个很坏的分割(反序亦然),而且会花费O(N^2)时间却什么都没做。
还有一种方法是使用随机数生成,但这会花费额外的时间代价,所以也不可取。
这里采用的是三数中值分割法(Median-of-Three Partitioning)。如果是想要最好的分割,自然是对半分,即选取中值作为枢纽元,但中值的计算又要付出代价,所以这里直接选取三个元素并将其中值作为枢纽元,这三个元素也不需随机,直接使用左端,中心位置,右端的三个元素即可。
分割策略
将枢纽元放在A[right-1]中,这样就可以定义两个下标i, j,分别指向A[left]和A[right-1],并相向而行,若下标指向元素同时不符合条件(A[i]应小于pivot,A[j]应大于pivot),则交换二者,而当i>j时,则分割完毕。对于与枢纽元相等的元素,这里也进行了交换。
对于小数组($N\le20$),快排不如插入排序好,所以可以define一个截止范围(cutoff range),数组大小小于时则使用插入排序,也避免了数组过小三数中值无法正确运行的情况。
src
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class quickSort {
private:
inline int median(vector<int> &arr, int left, int right) {
int med = (left + right) / 2;
if (arr[left] > arr[med])
swap(arr[left], arr[med])
if (arr[med] > arr[right])
swap(arr[med], arr[right])
if (arr[left] > arr[med])
swap(arr[left], arr[med])
swap(arr[med], arr[right - 1]);
return arr[right - 1];
}
void qsort(vector<int> &arr, int left, int right) {
if (right - left >= CUTOFF) {
int pivot = median(arr, left, right);
int i = left, j = right - 1;
while (i < j) {
while (arr[++i] < pivot) {}
while (arr[--j] > pivot) {}
if (i < j)
swap(arr[i], arr[j])
}
swap(arr[i], arr[right - 1]);
qsort(arr, left, i - 1);
qsort(arr, i + 1, right);
} else {
insertSort(arr, left, right);
}
}
void insertSort(vector<int> &arr, int left, int right) {
for (int i = 1; i <= right; ++i) {
int temp = arr[i], j;
for (j = i; j > 0 && arr[j - 1] > temp; --j)
arr[j] = arr[j - 1];
arr[j] = temp;
}
}
public:
vector<int>& sort(vector<int> &arr) {
if (!arr.size())
return arr;
qsort(arr, 0, arr.size() - 1);
return arr;
}
};
|
时间复杂度
最坏的情形是枢纽元始终是最小的元素,递推式为
$$T(N)=T(N-1)+cN, N>1$$
此时时间复杂度为$O(N^2)$;
最好的情形是枢纽元恰巧位于中间,递推式为
$$T(N)=T(N/2)+cN, N>1$$
此时时间复杂度为$O(N\log N)$;
平均情形时假设子数组的大小都是等可能的,为$1/N$,则递推式为
$$T(N)=\frac{2}{N} \left[\sum^{N-1}_{j=0}T(j)\right]+cN$$
此时时间复杂度为$O(N\log N)$
Refernce
《数据结构与算法分析——C语言描述》,Mark Allen Weiss
For More
Mergesort
Quicksort
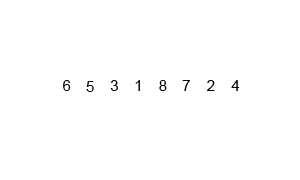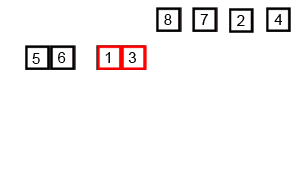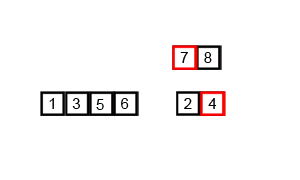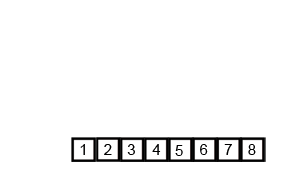

评论